De hydrologie horizontaal

Uit het KRW-doel geformuleerd door de waterleidingbedrijven, en de wens van de waterleiding bedrijven om drinkwater te kunnen maken voor minimale kosten, volt dat deze bedrijven gelet op de mechanismes van de groei van gewassen het assimilatie predicaat moeten voldoen, om kristalhelder water te kunnen winnen en de natuur te kunnen herstellen. Dat stelt eisen aan het interval {l,h} waarin de grondwaterspiegel hmv(t), ten opzichte van het maaiveld zich mag bewegen. Omdat meerdere wetenschappelijke vakgebieden samenkomen in één probleem: het herstellen van de natuur, lijkt het alsof het probleem dat we ons stellen niet oplosbaar is. Dat is gelukkig niet waar, maar de huidige onderzoekers lopen wel steeds tegen grenzen aan, die uitsluitend te verleggen zijn door meer samenwerking over de grenzen van vakgebieden. Gelukkig is een heel groot deel van datgene dat nodig is, al ontwikkeld, we moeten nu de laatste stap zetten door in alle winvelden het assimilatie predicaat goedkoop realiseerbaar te maken. Daarbij zijn hoogwaardige winvelden onmisbaar, niet alleen voor Nederland, maar voor alle landen die merken dat een verantwoorde winning van drinkwater steeds moeilijker te verenigen is met landbouw. Als dat niet meer mogelijk is, zal er ongetwijfeld een massa emigratie uit landen ontstaan, die deze zaken niet zelf op orde kunnen krijgen.

In de inleiding laat ik zien dat het voldoen van het assimilatie predicaat ook van groot belang is voor het beheersbaar maken van extreem weer, en een aantal essentiële delen van het klimaat doel.

Waterbalans aan het maaiveld

We gaan een winveld ontwerpen voor een hydrologie horizontaal en gebruiken de volgende gegevens voor het bepalen van de realisatie conditie. De neerslag N(t) heeft een jaargemiddelde heeft van 0.8m, dat ik in drie gelijke delen {winbaar, assimilatie, kwel} verdeel. Bovendien is het porievolume van de bodem 1/3.

Het winveld A(R) heeft een effectieve winingsstraal R.

Het bijbehorende buiten winveld B(R) heeft een areaal A(2R)-A(R) = 3A(R) en omsluit A perfect.

De grondwateraanwas zonder kwel stroom, is:

A(R): {0.8-winbaar, 0.8-assimilatie, 0.8}={0,    0, 0.8}

B(R): {0.8.                   0.8-assimilatie, 0.8}={0.8, 0, 0.8}

Door herverdeling van grondwater van B naar A ontstaat een evenwicht als bij communicerende vaten.

De winningsverlaging

De bijbehorende verlaging in A wordt de winningsverlaging genoemd en heeft als waarde ¼ N = 0.2m. De bijbehorende puntspreidfunctie kunnen we berekenen met een polynoom benadering, als de oneindig herhaalde convolutie van de cilinder C(R) met een hoogte van 0.2m met zichzelf.

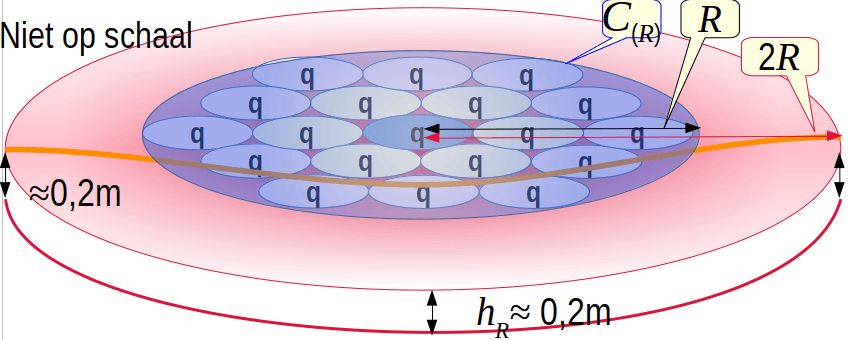
Verlaging door assimilatie

De globale gewasverdamping heeft een zeer grote overeenkomst tussen groepen gewassen, voorbeelden zijn: grasland en bos. Maar er zijn ook verschillen. Daarbij draait alles om de classificatie van de stofwisseling per gewas, zoals te zien is in de onderstaande afbeelding.

Bron: Publieksvoorlichting Duitsland

De gewasverdamping gaat gelijk op met de opbrengst van zonnecellen. De gemiddelde gewasverdamping is in het groeiseizoen groter dan de gemiddelde grondwateraanwas. Dit impliceert dat we op een locatie (x,y) te doen hebben met een grondwaterstandsverloop h(x,y)(t), dat een maximale waarde heeft vlak voor, en een minimale waarde, vlak na het eind van het teeltseizoen, voor alle (x,y) in het onbegrensde winveld W dat onderverdeeld kan worden naar delen met gewassen met een zelfde soort stofwisseling. Ook hier zal een herverdeling van grondwater van het ene deel naar het andere ontstaan en ook een evenwicht als bij communicerende vaten.

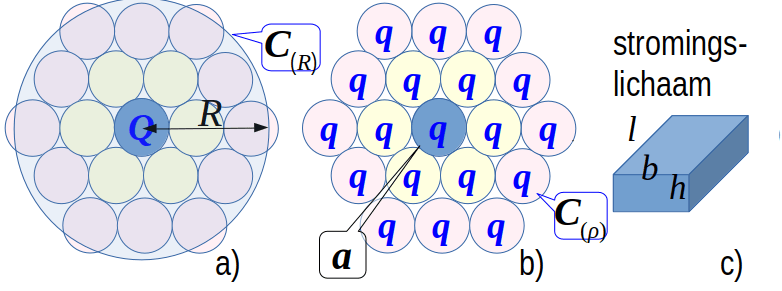
Er zal een golfvoortplanting ontstaan als de winbare neerslag N(t)A in de jaarcyclus in onbalans is met Q(t).

De beschreven meekoppeling is verantwoordelijk is voor het ontstaan van een golfvoortplanting in a) doordat het grondwater in de cilinder C(ρ) al overwegend verticaal gewonnen wordt, terwijl dat in de cilinder C(R) nog niet het geval is en ook nauwelijks zal gebeuren. Daardoor ontstaat een golfvoortplanting met een grote amplitude die kan oplopen van 0.8m tot 1.6m voor de grotere winvelden, die het voor de grootschalige winning van grondwater in a) ondoenlijk maakt om kleine assimilatie verliezen te realiseren.

Gespreide winning

In dit geval is de winning beperkt tot het winveld A waar het debiet Q(t) voor alle (x,y) in A en (t) stationair wordt gewonnen. Voor de details zie de waterbalans aan het maaiveld.

Let echter goed op voor een hydrologie hellend is alles, op een grote schaal, anders.

Het winveld wordt, in de wetenschap dat het water de weg van de minste weerstand zal volgen, opgedeeld in  cilinders C(ρ) waarbinnen de Laplace voorwaarden worden voldaan. De cilinders hebben een hoogte D en een straal ρ ≈ 3D. Maar homogeniteit is niet nodig.

Gelaagde watervoerende lagen kunnen we homogeniseren, door slecht doorlatende lagen in de verticale richting uit te rekken om zo een homogeen systeem van lagen te vormen ten behoeve van de berekening van de schaal ρ, daarbij neemt de dikte D toe, en krijgt de schaal parameter ρ een grotere waarde.

Stationaire transportverlaging

Grondwater stroomt niet zomaar naar een centraal punt in een winveld waar een zeer krachtige pompput opgesteld staat om het debiet Q(t)=A/a q(t) te kunnen winnen. Om de kosten van de leidingen uit te sparen, die nodig zijn om grondwater gespreid te kunnen winnen, wordt een transporttrechter gevormd, die het grondwater de weg wijst naar de pomp put(ten) door middel van gradiënten, die samen een trechter vormen. De dynamiek van de vorming van die trechter wordt beschreven door de grondwaterformule van Theis.

De stationaire transportverlaging mag, gelet op de zeer sterke niet lineaire assimilatie curve bij g.l, niet gebruikt worden, om het assimilatie verlies te berekenen, dat verlies wordt ook de droogte schade genoemd.

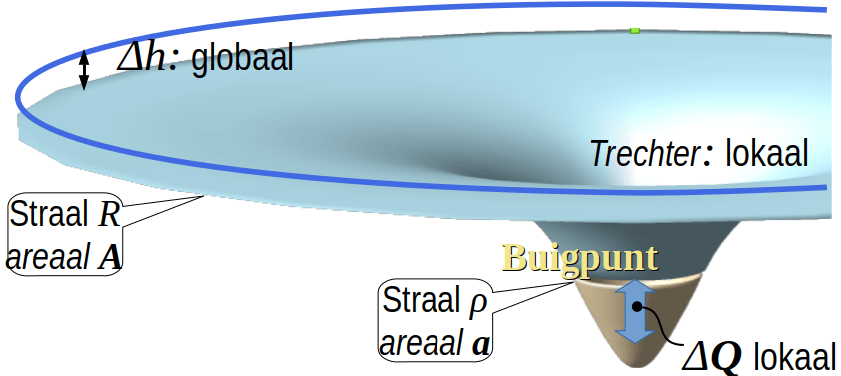
Als het evenwicht tussen het aanbod N(t)A en de vraag Q(t) verstoort, en dus niet-stationair is, passen de gradiënten in de transporttrechter niet meer voor alle (t) bij de gradiënten in de cilinder C(ρ), die in de watervoerende laag ontstaat als gevolg van een acute verandering tussen vraag en aanbod. Omdat het grondwater de weg van de minste weerstand volgt, zal een grondwaterspiegel, met een overwegend horizontale stroming, ergens in het winveld, ooit over moeten gaan naar een grondwaterspiegel met een een overwegend verticale stroming.

De implicatie hiervan is dat de differentiaal vergelijking die heeft geleid tot de transporttrechter, en is opgesteld onder de aanname dat de Laplace voorwaarden voldaan worden, niet geldig is, buiten de cilinder C(ρ). Daardoor komt de transportverlaging op een schaal groter dan ρ, niet meer overeen met de eigenschappen van de watervoerende laag binnen de cilinder C(ρ).

Het kost enige tijd voordat er een nieuw evenwicht ontstaat. Daardoor zal er een overgang ontstaan naar een andere transporttrechter. Zolang die overgang vele jaren duurt, wijkt de vorm van de transporttrechter, ook tijdens die overgang, niet al te veel af de stationaire transporttrechter, maar de praktijk is echter dat de balans tussen vraag en aanbod aan het begin van het teeltseizoen al verloren gaat.

Elementaire puntspreidfunctie

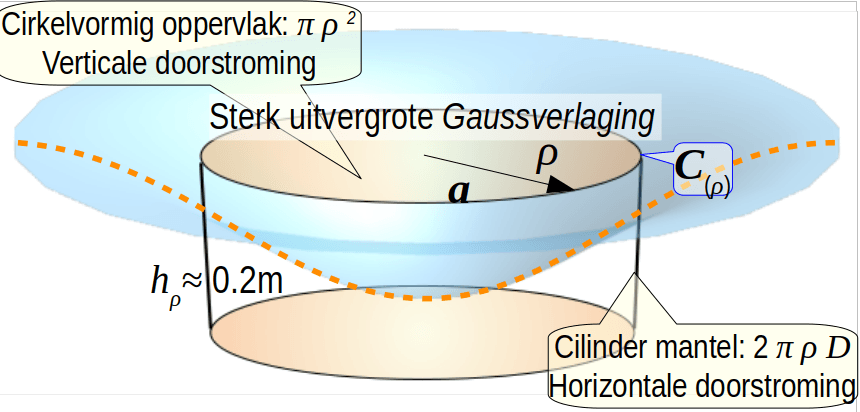
Bij een snellere overgang tussen vraag en aanbod, die elk jaar ontstaat, vormt zich in A een voor velen onverwacht golfverschijnsel. Omdat de straal van de cilinder C(ρ) zo is gekozen dat de weerstand voor een verticale doorstroming van de cilinder, zo goed mogelijk gelijk is aan de weerstand voor een horizontale doorstroming.

Daardoor is de vorm van de elementaire puntspreidfunctie van de watervoerende laag, met schaal ρ, constant, ongeacht de balans tussen vraag en aanbod. De implicatie is dat in a) lokaal de gradiënten zullen reageren op de balans tussen vraag en aanbod, terwijl er op afstand (nog) niets gebeurt. Dit gedrag is in strijd de met de Laplace voorwaarden die gebruikt worden om het systeem te beschrijven met een grondwaterformule of de tijdreeksanalyse, die stellen dat het watervoerende systeem lineair, plaats (x,y) en tijd (t) invariant en stabiel moet zijn. In het gespreide winveld b) wordt het grondwater op een driehoeksrooster direct gewonnen door gebruik te maken van de waterbalans aan het maaiveld. Daardoor blijft de verlaging beperkt tot de zeer kleine waarde van de winningsverlaging, groot ~0.2m. In dat geval valt in eerste aanleg het transport van grondwater binnen de effectieve winningsstraal R weg, en ook de instabiliteit, omdat het debiet q(t) van alle kleine pompputten gelijk is.

De elementaire puntspreidfunctie is van belang om de vrijheidsgraden van de grondwaterspiegel vast te leggen. We hebben die informatie nodig om met zo min mogelijk meetpunten, de grondwaterspiegel h(x,y,t) voor alle (x,y) en (t) als een vlak dat dynamisch van vorm kan veranderen voor te kunnen stellen door de segmenten van de best mogelijke polynoom benadering in (x,y) en (t) voor de gegeven meetpunten. Dit is het uitgangspunt voor de benadering van het benaderde vlak van de grondwaterspiegel op meerdere plaats (x,y) schalen (X) en tijd (t) schalen (T).

Deze informatie is tevens nuttig voor het versnellen van grondwater simulatoren, waarvan de meesten uitgaan van een rechthoekige doorsnijding (Δx,Δy) van de watervoerende laag, die doorsnijdingen hebben een vorm gelijkend aan die van gesneden aardappelen voor de frituur, die gebruikt worden om de differentiaal vergelijking numeriek op te kunnen lossen, langs de (x) en de (y) as. De heel expliciete doorsnijdingen (Δx,Δy) op een heel kleine schaal kunnen er zomaar voor zorgen dat het beschreven 'grondwater' bij zulke simulatoren evengoed niet de weg van de minste weerstand kan volgen omdat de verdeling van het grondwaterlichaam in doorsnijdingen in de hoogte Δz nog te grof is.

Die problemen ontstaan niet indien de grondwaterspiegel wordt gemeten, met de elementaire puntspreidfunctie als middel om van een paar discrete punten, over te kunnen gaan op een continue vlak. Zo krijgen we de best mogelijke benadering van de dataset [x,y,h(t)] met een approximatie fout <1mm, ook als de Laplace voorwaarden niet voldaan worden, hetgeen impliceert dat we de eigenschappen van het actuele winveld, door meting hebben bepaalt ongeacht of de Laplace voorwaarden op de gegeven schaal geldig zijn. Als we een animatie maken observeren we [x,y,h](t) voor t in een interval {t1,t2}.

In plaats van een animatie kunnen we ook de hoogte van de grondwaterspiegel aanpassen voor alle (x,y) in het winveld.

Dit werkt voor een perfecte hydrologie horizontaal zonder dat we daarover na hoeven te denken, maar ook voor hellend en ook voor elke tussenvorm, in die gevallen moeten we een strategie hebben om ervoor te zorgen dat de grondwaterspiegel zich uitsluitend in het interval van volledige assimilatie zal bewegen en ook om de doorgaande trend om te keren.

Dynamische transportverlaging

Bij het stationaire geval ontstaan er al onverwacht grote assimilatie verliezen die zich manifesteren als mest verliezen naar de bodem.

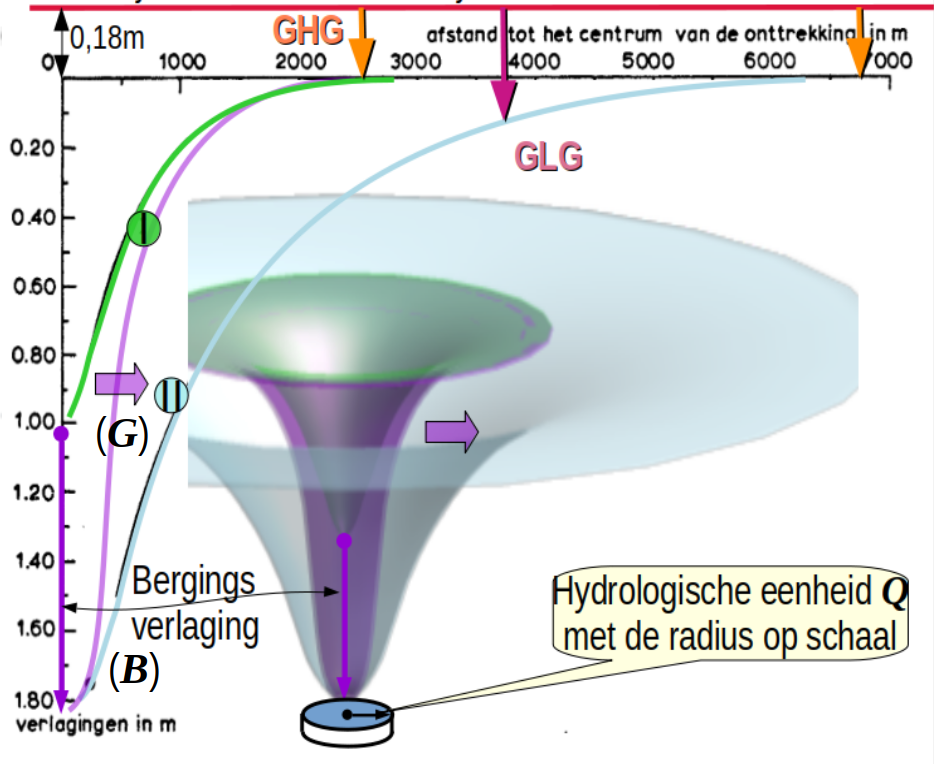
Dit is een belangrijk proces dat kenmerkend is voor een nieuw vakgebied, want als de gewasverdamping uitvalt, en dus ook de cyclus van het leven, ontstaat er een ongekend groot effect op de natuur en het klimaat.

De oneigenlijke som

De stationaire verlaging van een winveld is de oneigenlijke som van de winningsverlaging, groot 0.2m en de (optionele) transportverlaging die vaak wordt vergund met een waarde van 2m .. 4m. Ik spreek van een oneigenlijke som omdat er twee termen zijn waarvan,  als we een debiet Q(t) winnen, alléén de transportverlaging kan worden geëlimineerd. We kunnen beide termen ook weer samenvoegen, maar dat moeten we zo doen dat we de transportverlaging volgens Dupuit, binnen de effectieve winningsstraal A(R), optellen bij de winningsverlaging over hetzelfde interval. Daardoor gaat de som op dezelfde manier naar 0 als de winningsverlaging. Hieruit volgt tevens dat het winbare water niet uit het oneindige komt maar voor ~¼ uit het winveld A(R) en voor ~¾ uit het buitenwinveld B, de ring rond A, tussen de straal R en 2R aangeduid met B(R). Daarbij gaan de verlaging van de elementaire puntspreidfunctie, de transportverlaging, en de toestroom van water uit het buitenwinveld B(R) door herverdeling van grondwater zonder discontinuïteit in elkaar over. Veel interessanter is het echter dat we een winveld kunnen maken zonder transportverlaging, door het winveld te spreiden.

Alle verlagingen

Alle verlagingen van de grondwaterspiegel zijn:

1. de winningsverlaging
2. stationair groot 0.2m,
3. dynamisch: variaties in vraag en aanbod en
4. globaal: door assimilatie van meststoffen,
5. de transportverlaging
6. stationair groot 2m .. 4m voor veel vergunde winvelden (Dupuit).
7. dynamisch
   (golfvoortplanting, Theis, de Laplace voorwaarden zijn niet geldig)

De dynamische winningsverlaging is klein omdat er geen versterking is bij een schadevrij winveld. Wie de tijd nodig voor het bereiken van een evenwicht tussen het winveld A en het buitenwinveld B, wil beïnvloeden, kan het getal 21 in factoren te ontbinden (1x3x7) en binnen de straal 2R over te gaan op Ai kleinere winveldjes, met ieder een eigen buiten winveld Bi(Ri) in zo'n geval wordt het areaal van het buiten winveld B niet groter. Dit kan belangrijk zijn om kosten te besparen.                                                                       

Animaties

Beelden zeggen meer dan 1000 woorden. In de medische praktijk worden vlakken in real time gereconstrueerd om, onder andere verstoppingen of zwakke plekken in bloedvaten op te kunnen sporen. Iets dergelijks kan natuurlijk ook in de hydrologie, om meer informatie over de dynamiek te verkrijgen die ontstaat als grondwater gewonnen moet worden, dwars door een lagensysteem met verscheidene diktes.

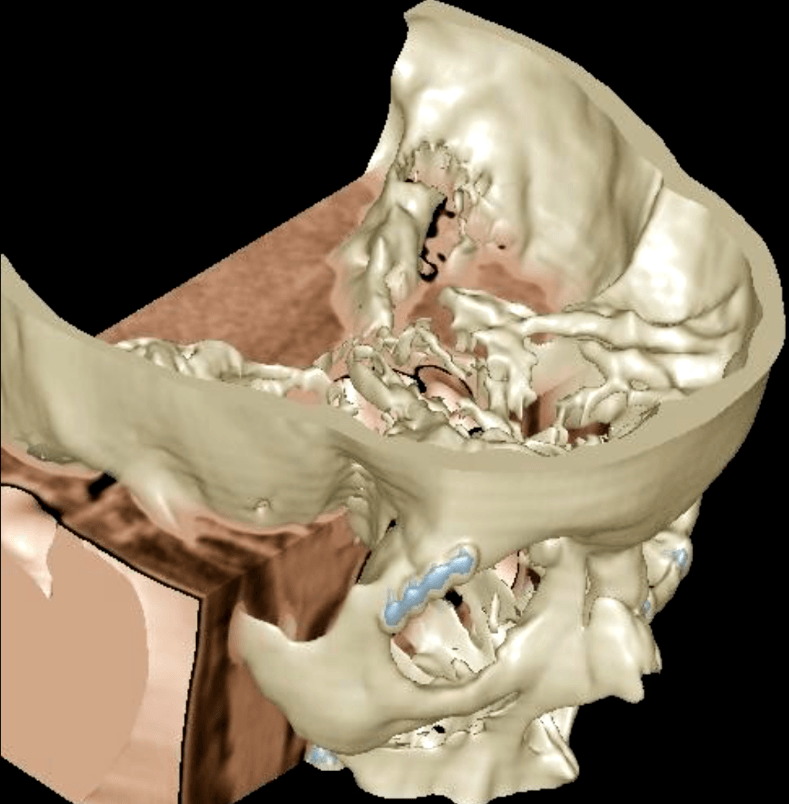
De bovenstaande afbeelding is een voorbeeld van zo'n medische toepassing uit 1995, waarbij volume veranderingen nog niet worden bestudeerd, maar wel een breuk van de schedel basis, vlak bij de oogkas, die met een plaatje en schroefjes (blauw) gerepareerd werd. In 1995 was het vakgebied der elektrotechniek al zover ontwikkeld dat Dr. M.K. Bosma, een systeem kon maken waarmee in real-time en met zeer hoge kwaliteit 3D medische beelden zichtbaar gemaakt konden worden op een gewone computer. Dit soort afbeeldingen, maken wel duidelijk wat je kunt doen met de elementaire puntspreidfunctie van het watervoerende lagensysteem en een groter aantal meetpunten dan gebruikelijk om een eenduidige reconstructie mogelijk te kunnen maken van de grondwaterspiegel h(x,y,t).

Er zijn vele mogelijkheden om het punt op de assimilatie curve te coderen door de kleur aan te passen, dat zien we bijvoorbeeld op de snijvlakken in de afbeelding waar de gemeten grijs-waarde, de dichtheid van het zachte weefsel, die het oppervlak van gelijknamige grijswaarde vastlegt in de onderliggende CT scan.

Terugblik

G.W. Bloemen ¹heeft als eerste de winningsverlaging gemeten voor het winveld het Klooster in Hengelo Gld. en gaat, al in 1973, ook in op de golfvoortplanting.

Al in 1998 werd het effect van golfvoortplanting op de vorm van het grondwaterstandsverloop gemeten, bij onderzoek naar ²verdroging in Limburg, veroorzaakt door het winveld bij Helmond: de Stippelberg. De ³hydrologen staan op het punt om een belangrijke ontdekking te doen, als ze in 2002, vier jaar na de eerste publicatie, uit 1998 schrijven:

Dat de drinkwaterwinning één van de oorzaken is kwam als een verrassing, omdat er een actief beleid gevoerd wordt om deze onttrekkingen terug te dringen…

M.H. Zwamborn ontdekte dat de grondwaterspiegel bij de pompput een snelle overgang maakt tussen stationaire oplossingen volgens de grondwaterformule van Dupuit, waardoor de grondwaterspiegel voor een hydrologie horizontaal, een blokgolf en op andere plaatsen een driehoeksgolf werd met heel duidelijke oneven harmonischen. Deze waarneming impliceert ook dat de Laplace voorwaarden niet geldig zijn voor de watervoerende laag, doordat het water binnen deze zeer dunne laag altijd de weg van de minste weerstand zal volgen, hetgeen impliceert dat een watertekort eerst uit de in omgeving van de pompput gewonnen wordt, en dat daarna de winningsstraal steeds groter zal worden. Er ontstaat daarbij ook een teruggaande golf.

De indertijd razend populaire waterbesparing campagnes worden ook anno 2024/2025 weer van stal gehaald, ondanks het feit dat door waterbesparing aan de kraan, tot 2002 nog nooit een probleem opgelost werd. De bladen van de persgroep schijven dat je, om water te besparen, toch maar beter niet onder de douche moet plassen! Je moet er wat voor over hebben, plassen onder de douche om water te besparen...

Het schadevrije winveld maakt in één klap een eind aan het fabeltje van de achtergrondverlaging, dat prof. M.P.F. Bierkens als mediator namens de NHV als volgt omschrijft:

Als je een deel van de verlaging verklaart uit de achtergrondverlaging, dan heeft dat veelal een groot effect op de berekende schade van een winning.

Het doet echter niet ter zake welke schade de drinkwatersector berekent, zolang ze maar de droogteschade berekenen, volgens art. 7.18 waterwet. Ik spreek liever over het assimilatie verlies, omdat daaruit blijkt dat het om schade gaat aan de groei van de gewassen, die ook een schade aan de kringloop van het leven veroorzaken. Het grote effect waar Bierkens aan refereert, ontstaat omdat de assimilatie nagenoeg volledig uitvalt in het interval g.{ll, l} dat in veel gevallen niet groter is dan 0.25m. Daardoor kan het voorkomen dat de ⁴berekende schade 80% kleiner is dan de droogte schade. Dit impliceert ook dat in z'n geval 0.2/0.25 ofwel 80% en in voorkomende gevallen, zelfs 95% van de mest, bedoeld voor de groei van het gewas, naar de bodem verloren gaat.

Dat is heel wat anders dan het kristalheldere productie water afkomstig van schadevrije winvelden.

In zo'n geval moet er ook iemand zijn die z'n werk niet goed heeft gedaan. Een medewerker van de Alterra meetploeg werd, ⁵geheel ten onrechte, ontslagen. Als ⁶iedereen daarmee in zou stemmen, zou de weg vrij zijn voor de grootschalige toepassing van de zeer profijtelijke achtergrondverlaging, in combinatie een onbeheersbaar assimilatie probleem, dat zorgt voor zeer grote mest verliezen naar de bodem.

Je kunt wel denken dat mest een agrarische oorsprong heeft, maar als dat klopt, dan waren er nooit vegetarische Dinosauriërs geweest.

Het was prof. J.J. de Vries die, het schaal probleem in het vakgebied van de hydrologie benoemde, zonder daar een invulling aan te geven. Voor versterkingsfactoren A/a veel groter dan 1, zijn er als gevolg van golfvoortplanting  delen van de watervoerende laag die als gevolg van het evenwicht tussen vraag en aanbod, verticaal doorstroomd worden. Wie liever geen onbeheersbaar mest probleem, wil hebben, en het nut van schadevrije winvelden, nog niet goed genoeg begrijpt, moet teruggaan naar het begin van dit hoofdstuk, waarin ik de groei van gewassen (planten) uitleg, aan de hand van de modellen die binnen de FAO waren ontwikkeld, die prof. R.A. Feddes nader heeft uitgewerkt om de droogteschade uit te kunnen rekenen. Vanuit de optiek van de drinkwatersector is het nut van de schadevrije winvelden, het compleet wegvallen van de problematiek rond de compensatie vergoedingen en de eliminatie van het onbeheersbare mest probleem, het beheersen van de bodem chemie, allemaal zaken die onoplosbaar zijn zonder schadevrije winvelden.

1. G.W. Bloemen, De berekening met een waterbalansmodel van de daling van freatisch grondwater als gevolg van grondwater winning, ICW Nota 758, aug. 1973.
2. M.H. Zwamborn, C. Maas, P.K. Baggelaar, Box-Jenkins trendanalyse niet altijd toepasbaar, H2O, 1, 1998
3. C. Maas, J.R. von Asmuth, Tijdreeksanalyse grondwaterstanden 1975 – 2002, Effectiviteit van het standstill beleid van de Provincie Limburg. KWR 03.092
4. C. Maas, Valkuilen in de tijdreeksanalyse: Het geval Terwisscha, Stromingen 18 (2012), nr 2
5. Zie: PS 2012/775
6. M.P.F. Bierkens, De achtergrondverlaging op de voorgrond, Presentatie NHV Najaarsbijeenkomst, 28 november 2013
   

In de hydrologie zijn andere aspecten belangrijk, zoals de golfvoortplanting die ontstaat bij een onbalans tussen vraag en aanbod, omdat de Laplace voorwaarden niet geldig zijn, of de hoeveelheid bodemvocht die in de onverzadigde zone door adhesie blijft hangen na een  regenbui. Daar zijn al wel praktijkregels voor in het geval van beregening, maar als je een schadevrij winveld wilt ontwerpen, wil je ook dat het resultaat gemonitord kan worden. Als dit soort 3D reconstructies veel eerder waren toegepast op grondwaterspiegels van een systeem waarvoor de Laplace voorwaarden niet geldig zijn, dan zou een flink aantal vakgebieden in de wetenschap zich nooit dilettantisch ontwikkeld hebben, immers beelden zeggen meer dan 1000 woorden.

Op vergelijkbare manier kun je in één oogopslag, gecodeerd op de grondwaterspiegel, zien wat zich afspeelt in de bodem. Dat is van cruciaal belang voor het begrijpen van de processen in de vakgebieden van de ... hydrologie, ecologie, bodemchemie, meteorologie, waardoor we extreme droogte, natuurbranden en onverwachte overstromingen in het hart van Europa, en onnodige veranderingen in het klimaat, aan kunnen pakken.

We moeten elkaar niet aanvallen en ook niet afvallen, maar het is wel cruciaal dat een nieuw vakgebied zich kan ontwikkelen vrij van dilettantisme.

Daardoor kunnen we volgen dat het gewas, bij droogte, eerst nog het water opneemt van het vocht dat zich door adhesie hecht aan de bodem. Als we dit soort technieken hadden gebruikt in de hydrologie en de ecologie, dan was er nooit sprake geweest van dilettantisme.

De eerlijkheid gebied echter ook te zeggen dat dit pas sinds zeg 1995 mogelijk is, en in die tijd was er evengoed behoefte aan vergunde winvelden.