Hydrologie horizontaal
Als de grondwaterspiegel h(x,y,t) in de nul-toestand horizontaal en vlak is er in de nul-toestand, geen horizontale stroming van het grondwater in het winveld. Bij horizontaal en lensvormig worden in de nul-toestand, de sloten in de omgeving gevoed door het kwelwater dat een grondwaterlens heeft gevormd. De stationaire verlaging van de grondwaterspiegel h(x,y,t), ontstaat als de oneigenlijke som van de stationaire winningsverlaging die 0.2m groot is, voor horizontaal en 0.4m voor horizontaal en lensvormig en de (optionele) stationaire transportverlaging.
Eigenschappen van winvelden
Basis kennis die niet klopt
Iedere hydroloog leert dat de grondwaterstroming de richting van de gradiënt van de grondwaterspiegel volgt, en dat de stroomsnelheid ook sterker wordt, naarmate de gradiënt grotere waarden aanneemt. Die bewering is bij zeer goede benadering correct, binnen de schaal ρ van een homogene watervoerende laag, maar zodra voor de effectieve winningsstraal R van het winveld, geld dat R > ρ dan is de aanname dat het grondwater met een zuiver horizontale stroming naar de pompput stroomt niet langer geldig. De kern van de zaak is, dat het grondwater, zeker in het dynamische geval, geen specifieke stroombanen volgt. Het resultaat is dat schade vrije winvelden niet ontworpen kunnen worden met (klassieke) grondwaterformules en ook niet met de tijdreeksanalyse en aanverwante technieken die aannemen dat de Laplace voorwaarden geldig zijn, het probleem is dat de Laplace voorwaarden geen vergelijkingsoperator zoals < kennen, die de schaal parameter ρ vastlegt.
Ik zal nog laten zien hoe deze techniek ook gebruikt kan worden met niet homogene watervoerende lagen.
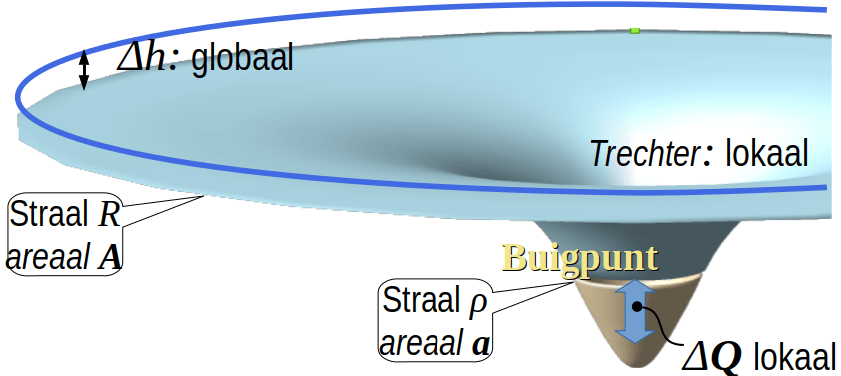
De schaal parameter
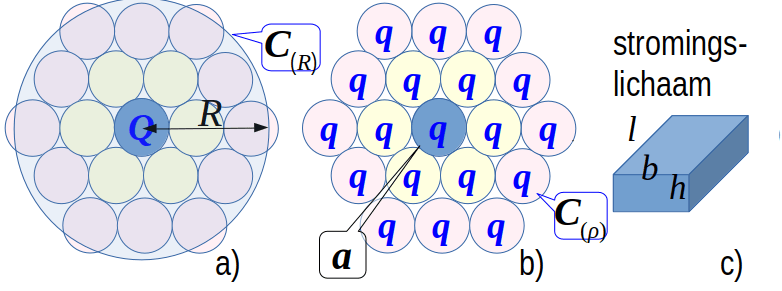
De cilinders C(ρ), met de hoogde D van de watervoerende laag en een pompput q(t) en areaal a=πρ2, hebben als speciale eigenschap dat de weerstand voor een verticale doorstroming, van dezelfde ordegrootte is als de weerstand voor een horizontaal-radiale doorstroming van het winveldje met areaal a, deze eigenschap definieert de schaal parameter ρ ≈ 3D van de watervoerende laag.
De effectieve winningsstraal
De cilinder C(R) spant het primaire winveld, met areaal A op, waarbij A=πR2, en R de effectieve winningsstraal.
De cilinder C(2R) spant het areaal A + B op met B het secundaire winveld, dat als een ring om A heen ligt.
Vraag en aanbod
Het evenwicht tussen vraag en aanbod wordt gegeven door: q(t) ≈ Nwinbaar(t) a, met het areaal a=πρ2, daarbij is de vraag (het linkerlid) als regel niet gelijk aan het aanbod (het rechter lid van de vergelijking).
Grootschalige winvelden
Bij grootschalige winvelden met een enkele locatie (x0,y0) waarop pompputten opgesteld zijn geldt: Q(t)=A/a q(t), voor A/a > 1 spreken we over een grootschalig winveld.
In een grootschalig winveld ontstaat naast een stationaire winningsverlaging, ook een stationaire transportverlaging.
Voordat het winveld in gebruik is, is de grondwaterspiegel horizontaal, maar de pompput wil het debiet al Q winnen op het moment dat er nog helemaal geen duidelijk onderscheid is tussen winning en transport. Daardoor wordt grondwater dat al aanwezig was in de watervoerende laag gewonnen. Bij dat proces vormt zich de winningsverlaging, eerst met een straal ρ en een verlaging die toeneemt tot ~0.2m, daarna wordt de effectieve winningsstraal R groter, terwijl gelijktijdig de transporttrechter, die aansluit op de effectieve winningsstraal R, wordt uitgediept. Elke keer dat een groter debiet Q wordt vergund zal dit laatste proces verder doorzetten: de winningsstraal R wordt groter en de transporttrechter wordt dieper. Nieuwe stationaire toestanden worden bereikt binnen 5 jaar en de effectieve winningsstraal doorloopt waarden: in {ρ(D) ... R(Q)}. Bij een hydrologie hellend die ontstaat als de grondwaterspiegel meer dan 1‰ helt, ontstaat een doorgaande trend, daarbij wordt veel meer water onttrokken aan de watervoerende laag, waardoor de evenwichtstoestand later optreedt.
De oneigenlijke som
De stationaire verlaging van de grondwaterspiegel h(x,y,t), ontstaat als de oneigenlijke som van de stationaire winningsverlaging en de optionele stationaire transportverlaging.
Het dynamische geval
In het dynamische geval wisselen verticale en horizontale stromingen elkaar, als functie van het evenwicht tussen vraag en aanbod, af bij de pompput. Daarbij wordt als ΔQ positief is, lokaal overmatig veel grondwater gewonnen, dat via een autonome verdeling van grondwater, die samengaat met een golfvoortplanting, weer aangevuld wordt.
Opschalen en mest verliezen
Het opschalen van het debiet Q van een grootschalig winveld kan door een extra pompput bij te plaatsen. Maar dit gaat natuurlijk wel gepaard met een grotere effectieve winningsstraal en een diepere transporttrechter. Door toepassing van het assimilatie predicaat ontdekken we al gauw dat dit, zodra de grondwaterspiegel beneden h3(x,y) komt, gepaard gaat met grote mest verliezen naar de bodem over een groter gedeelte van het winveld A.
| Winveld (Vitens) | Qvergu | Qverko | % |
|---|---|---|---|
| Herikerberg | 330.000 | 405.199 | 123 |
| Manderveen | 300.000 | 406.642 | 136 |
| Weerselo | 85.000 | 108.089 | 127 |
| Sint Jansklooster | 500.000 | 618.260 | 124 |
| Witharen | 500.000 | 513.787 | 103 |
| Hoge Hexel | 250.000 | 299.214 | 120 |
| Wierden | 800.000 | 936.366 | 117 |
| Nijverdal | 600.000 | 641.581 | 107 |
| Holten | 250.000 | 286.771 | 115 |
| Engelse Werk | 420.000 | 424.619 | 101 |
| Archemerberg | 400.000 | 426.290 | 107 |
| Rodenmors | 150.000 | 152.280 | 102 |
In de bovenstaande tabel zien we dat Vitens in Overijssel de vergunde hoeveelheid in de maand juli al nagenoeg overal al flink overschrijdt. In het begeleidende 1artikel in de Stentor staat dat deze overschrijding noodgedwongen was, maar door schade vrije winvelden te gebruiken, blijkt dat we deze debieten ook met een stationaire winningsverlaging van 0.2m kunnen winnen, met daarbij opgeteld een dynamische verlaging over zeg ½ jaar die bij een schadevrij winveld over het hele winveld even groot is. Die waarde is eenvoudig te berekenen en ook in het ontwerp in te passen. Het ontwerpcriterium moet zijn dat de grondwaterspiegel h(x,y,t) zich zal bewegen in het interval van volledige assimilatie, conform het assimilatie predicaat. Op deze manier kunnen schadevrije winvelden worden ingezet om grootschalige winvelden te maken zonder last te hebben van de vele schadelijke effecten van de transportverlaging. Ook voor hellend bestaan dit soort ontwerpregels.
We moeten het aanmoedigen dat winvelden die echt zeer kleine schades veroorzaken, meer en vooral ook laagdrempelig, toegepast en ook vergund zullen worden.
Dat is goed voor de drinkwatersector, de landbouw, de natuur en het klimaat, als eerder aangegeven.
- A. ten Cate, Vitens pompte noodgedwongen meer water op dan mocht tijdens extreme droogte, De Stentor, 21-09-18, 18:41
Gedrag in de jaarcyclus
Het evenwicht tussen vraag en aanbod is in de jaarcyclus van nature al onevenwichtig. Ook in de jaarcyclus zelf zal er eerst rond de pompput een met A/a versterkte verlaging optreden als in fig. 1, bij een vergroting van het actuele debiet met ΔQ. Dit wordt verder uitgewerkt in het hoofdstuk de dynamiek van winvelden.
Merk ook op dat de vorm van de grondwaterspiegel niet verandert als er een regenbui valt, tenzij er in de periferie van het winveld een kwelstroom ontstaat.
Schadevrije winvelden
Bij de opbouw van een schadevrij winveld, plaatsen we cilinders C(ρ) zo dicht mogelijk op elkaar in een driehoek rooster, binnen de cilinder C(R). Dan hebben we een schadevrij winveld gemaakt, zonder transportverlaging, dat het debiet Q(t) kan winnen, met een winningsverlaging van slechts 0.2m. Met zo'n winveld kan het natuurdoel probleemloos gerealiseerd worden. Daarbij is de maximaal toegestane stikstof concentratie te koppelen aan de schaal parameter ρ, die daardoor, samen met een vergelijkingsoperator zoals <, de rol heeft van een ontwerpparameter van het winveld.
Met zo'n winveld is drinkwaterwinning heel goed (koop) mogelijk en goed in te passen in de bestemmingsplannen, van agrarisch terrein, bos en open natuurterrein, en bebouwd terrein, terwijl tevens het natuurdoel gerealiseerd zal worden voor alle (x,y) en (t). Het evenwicht tussen vraag en aanbod in de jaarcyclus bepaalt het actuele grondwaterstandsverloop, dat zo ontworpen moet worden dat het binnen het interval van
volledige assimilatie zal blijven van het gewas g(x,y), ook in een jaar zonder winbare neerslag. Omdat er geen transporttrechter is en ook omdat de in eerste aanleg verticale grondwaterstroming niet grootschalig van richting verandert, worden er zeer zwakke eisen gesteld aan de statistiek van het debiet
Q(t) en de neerslag
N(t). De details zijn te vinden in het volgende hoofdstuk.
De winningsverlaging
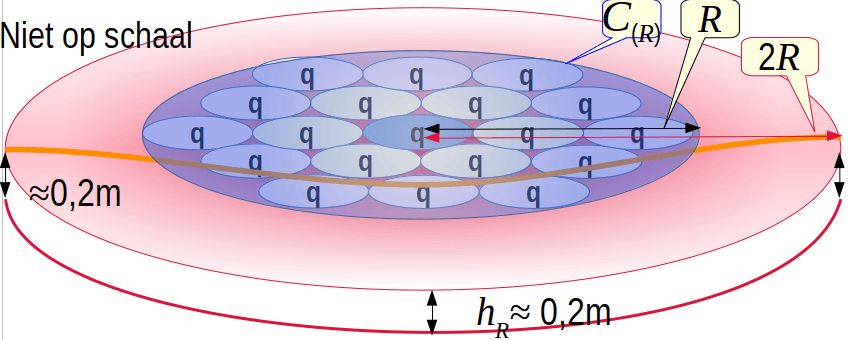
Binnen de cilinder van de effectieve winning straal C(R) winnen pompputten met een debiet q(t) = a/A Q(t) gespreid de winbare neerslag Nwinbaar(t) A, met A=πR2 het areaal van het winveld. Naast het winveld A is er ook een secundair winveld B dat via herverdeling van grondwater bijdraagt aan de winning. Het secundaire winveld ligt tussen R en 2R en heeft een areaal B = 3A.
Ik verdeel de neerslag N als een reservering op in drie gelijke delen {Nwinbaar, Nassimilatie, Nkwel} en stel de aanvullende eis dat die verdeling behouden blijft bij winning {Qgewonnen, Qgeassimileerd, Qkwel} door {pompputten, gewas, uittreden van kwel} daarbij geldt de volgende ordening [winbaar > assimilatie > kwel].
Water dat gewonnen en verkocht is, is niet meer beschikbaar voor assimilatie, maar er geld ook dat niet alle water geassimileerd kan worden. Bovendien is water dat heeft bijgedragen aan de groei (eventueel via beregening) niet meer beschikbaar is voor kwel.
Bij een porositeit van 1/3 en na aftrek van de gespreid optredende assimilatie, die in landbouwgebieden en natuurgebieden van dezelfde ordegrootte is, moet het ontwerpproces van de winvelden A en B die het mogelijk maken om een volledige assimilatie & gewasverdamping en het behoudt van de kwelstroom te realiseren, opdat er kristalhelder grondwater zal ontstaan. Als we ook het zure sulfaatbodem predicaat realiseren, kunnen ook de bijbehorende processen, die een grote invloed hebben op bodemchemie, beheersbaar maken.
Door de winning ontstaat als we met stationaire waarden rekenen, een grondwateraanwas op jaarbasis groot {0, 0, 0.8}m in A en {0.8, 0, 0.8}m in B, met als gevolg dat het verschil tussen de jaarlijkse grondwateraanwas in A en B 0.8m/jaar is. Omdat de oppervlakken van A en A + B zich verhouden als 1 : 4 zal er bij een verlaging in het winveld A van N/4 = 0.2m, een stationaire oplossing ontstaan. Dat G.W. Bloemen al in 1973 0.18m heeft gemeten komt mede omdat in 1973 het jaargemiddelde van de neerslag, met 0.75m, iets kleiner was dan de huidige waarde van 0.8m.
Door deze manier van werken wordt in
A een zuiver verticale stroming afgedwongen, over de kleinst mogelijke afstand
D in de watervoerende laag. Dit is belangrijk omdat de Laplace voorwaarden die stellen dat het systeem
lineair,
tijd (t) en
plaats (x,y) invariant, en
stabiel is,
niet geldig zijn voor grootschalige dunne watervoerende lagen, waarbij de cilinder
C(R), wordt bedekt met A/a cilinders
C(ρ). Dat komt doordat het grondwater van nature de weg van de minste weerstand zal volgen.
Tijdens de vergaderingen, die tot stand kwamen door bemiddeling van prof. M.P.F. Bierkens, gewijd aan de achtergrondverlaging, stelde prof. J.J. de Vries dat er sprake moest zijn van een schaal probleem. We weten nu dat dat ontstaat doordat A/a > 1. Een schaal probleem treedt ook op bij het zien van de Penrose driebalk, die ik hier als logo gebruik. Bij elke hoek weten we hoe de driebalk eruit ziet, maar als we een stap terug doen, en de hele driebalk zien, raken we in verwarring, er klopt iets niet. De bekende graficus M.C. Escher gebruikt dit fenomeen om een waterval te tekenen die zichzelf voedt. In de hydrologie zorgt het schaal probleem via de schaal parameter ρ en de < operator, ervoor dat de Laplace voorwaarden niet geldig zijn.
Iedere hydroloog leert, dat de watervoerende laag voldoet aan de Laplace voorwaarden, maar juist dat klopt vanwege het schaal begrip niet voor dunne watervoerende lagen.
De Laplace voorwaarden zijn juist niet geldig zodra we grootschalige winvelden bestuderen. Dit heeft vergaande consequenties doordat grondwaterformules, de tijdreeksanalyse, superpositie van responsies, etc. van de hoogte van de grondwaterspiegel, en vele andere technieken, juist niet toegepast mogen worden, omdat de Laplace voorwaarden niet geldig zijn. De reden daarvoor is dat de grondwaterstroming de weg van de minste weerstand volgt. In fig. 2 b) volgt de stroming in elk areaal a de weg van de minste weerstand in elke cilinder C(ρ).
Door de introductie van de cilinders C(ρ) kunnen we een zuiver verticale winning van grondwater afdwingen voor alle (x,y) en voor alle (t) waardoor we weten dat Nwinbaar lokaal gewonnen wordt. Door achteraf de autonome herverdeling van grondwater door te rekenen met convolutie technieken, weten we dat daarbij, vanwege de beperkte dikte D van de watervoerende laag, in tweede instantie een 'zuiver' horizontale stroming op zal treden. Door zelf de regie te houden over de volgorde van de berekeningen kunnen we voor een beperkt aantal gevallen de formules voor de grondwaterstroming blijven gebruiken ook als de schaal ρ van het winveld dat zonder de beschreven regie niet toestaat.
Het feit dat de watervoerende laag, zelf niet voldoet aan de Laplace voorwaarden, hoeft niet te betekenen dat deelproblemen om die reden ook niet doorgerekend kunnen worden. We zijn in dat geval echter afhankelijk van voorkennis, die we op basis van de gegeven geometrie inbrengen. Om een winveld te maken dat de winningsverlaging realiseert, heb ik ervoor gekozen om de winning van grondwater door middel van een in eerste aanleg zuiver verticale stroming te beperken tot de effectieve winning straal R, met pompputten die niet meer winnen dan Nwinbaar, de winbare neerslag. Dit heeft als effect dat de netto grondwater aanwas in A en B verschillend is, waardoor van buiten de effectieve winning straal steeds meer grondwater via herverdeling van grondwater ervoor zal zorgen dat er een een nieuw evenwicht zal ontstaan.
Deze herverdeling veroorzaakt op zijn beurt een in eerste aanleg zuiver horizontale stroming, waarvan het resultaat met convolutie berekend kan worden. Als we hadden gekozen voor de superpositie van de punt spreid functies die bij de cilinders C(ρ) horen, dan zou er sprake zijn van een rand buiten de effectieve winning straal R, groot ρ. Bij het gebruik van convolutie wordt diezelfde rand gelijk aan R. Het is eenvoudig na te gaan dat dit het correcte antwoord is. De convolutie integraal, die veelvuldig wordt toegepast bij het berekenen van een respons die hoort bij een gegeven functie u en een punt spreid functie v, wordt beschreven als:
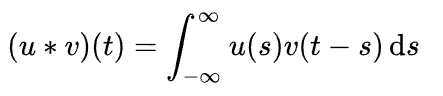
Hier zijn u en v functies van één gemeenschappelijk tijdstip t, het resultaat wordt gevormd als de convolutie * van u met v. Bij de berekening van de herverdeling van grondwater berekenen we (u * u * ...) door autocorrelatie. Deze berekening moet oneindig herhaald worden om de evenwichtstoestand te vinden. In het 1D geval geeft dit langs de stroomlijnen de opeenvolgende verlagingstoestanden als aangegeven in fig. 4 b). Een goed uitgewerkte animatie vinden we in de wikipedia.
Kenmerkend bij herverdeling van grondwater is dat bij een doorsnede uit een lijn winning het oppervlak onder een stroomlijn constant blijft. In het meer algemene geval blijft de waterbalans constant. Daarom sprak G.W. Bloemen uit de groep van prof. L.F. Ernst over de
waterbalansanalyse.

In het radiaal symmetrische geval ontstaat de onderstaande elementaire puntspreidfunctie van een pompput centraal geplaatst diep in een cilinder C(ρ).
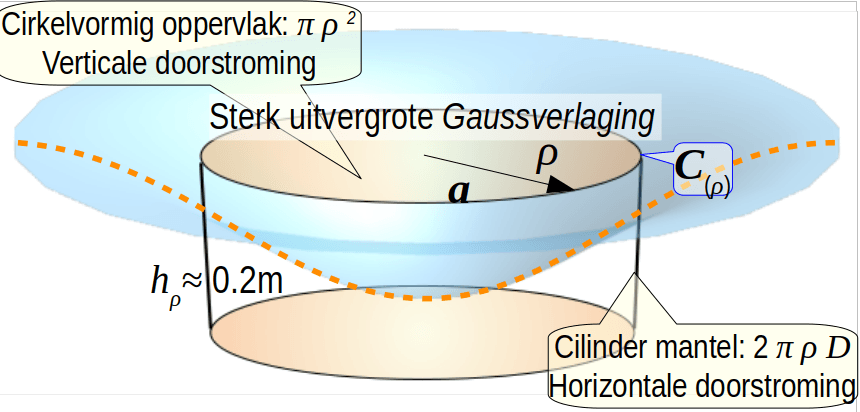
De transportverlaging
De stationaire transportformule van Dupuit kan afgeleid worden door voor alle stralen (r) tussen {ρ, R} het potentiaalverschil te berekenen over een cilindermantel met dikte δr als gevolg van een zuiver horizontale doorstroming, die voor alle (z), in het (x,y) vlak dezelfde doorstroming realiseert, voor het stationaire debiet Q. De integraal telt voor elke r en δr de potentiaal verschillen op.
Er wordt aangenomen dat de dikte D overal even groot is. Die aanname is vaak niet voldaan, stel; dat de dikte van de watervoerende laag 10m is terwijl de verlaging in het winveld 2m tot 4m is, dan ontstaan er grote fouten. Voorts wordt de stationaire oplossing beschreven, maar juist het dynamische gedrag is als regel problematisch, omdat de stoombanen snel bewegen van richting, als gevolg van de onbalans in het patroon tussen vraag en aanbod.
Het is bovendien belangrijk om nauwkeurig te werken, want:
Als je een deel van de verlaging verklaart uit de winningsverlaging (achtergrondverlaging), dan heeft dat, volgens prof. M.P.F. Bierkens, veelal een groot effect op de berekende schade van een winning.
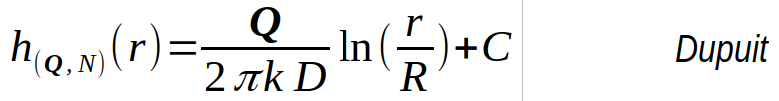
De intervallen 0<ρ<R<2R
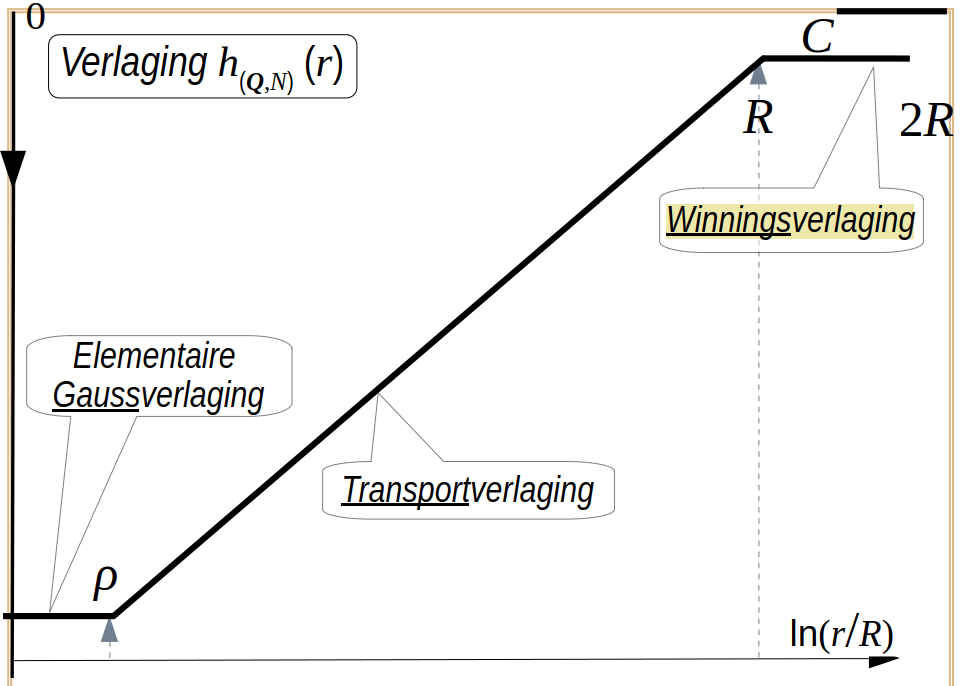
Voor 0 <= r < ρ is de vorm van de Gaussverlaging van groot belang, voor de gedetailleerde vorm, maar ook voor het dynamische gedrag. Voor ρ <= r < R moeten de winningsverlaging en de transportverlaging bij elkaar opgeteld worden. Voor R <= r < ∞ blijft nog slechts de winningsverlaging over, immers in beide gevallen gaat ¾ Q door de mantel van de cilinder C(R). Daardoor wint óók een winveld met een winningsverlaging en een transport verlaging alle grondwater uit z'n 2R omgeving van de pompput. Hiermee is ook het probleem van de winning van het water uit het oneindige, dat intrinsiek is voor een transportformule, opgelost.
G.H. Bloemen is al in 1973 zijn tijd ver vooruit met z'n ongekend nauwkeurige meetresultaten, die hij voor iedereen die zijn publicatie leest, toegankelijk maakt. Zoals het hoort. Maar de drie intervallen die ik hier onderscheidt, zijn niet in fig. 7. terug te vinden.
De transportgrafiek
Voor r = R geldt: ln (r/R) = ln (1) = 0, waardoor we de integratie constante C kunnen bepalen die overeenkomt met de achtergrondverlaging (≡winningsverlaging).
Een handige manier om meetresultaten met de transportformule van Dupuit zichtbaar te maken bestaat uit het gebruik van een lineaire schaal voor h(Q,N) en een ln (r/R) schaal voor de afstand (r) tot de pompput (Q) op de plaats (0,0) en asymptoten die de grafiek in 4 intervallen verdelen.
Let op dat ik de notatie
h(Q,N) gebruik om aan te geven dat
Q,N parameters zijn, met constante waarden. Merk op dat de neerslag
N helemaal niet voorkomt in de transportformule van Dupuit. De implicatie daarvan is dat de
transportformule van
Dupuit niet gebruikt kan worden om de
De dynamiek van winvelden
In het als droog gekarakteriseerde jaar 2018 was de verdeling van het water voor {winbaar, assimilatie, kwel} = {0.8, 0.8, 0.2}m, terwijl de mest verliezen naar de bodem, die gelijk zijn aan de opbrengstdepressie, 95% van de mestgift waren. Ondanks dat de drinkwatersector hierin een belangrijke rol heeft gespeeld, wil ik hen in bescherming nemen. Het was, niet alleen in Nederland, maar in heel Europa, heel gewoon dat alle mest verliezen naar de bodem voor lief genomen werden, met als gevolg dat ze bij het uitbreiden van vergunningen, wat ze nu ook weer willen doen, ongemerkt heel grote waarden konden aannemen. Weliswaar stelden de provincie bestuurders de winst op de eerste plaats, maar de drinkwatersector kon ook altijd winvelden goedgekeurd krijgen die net iets goedkoper realiseerbaar waren, waardoor het aspect van mest verliezen naar de bodem, niet fungeerde als de basis voor het ontwerpproces. Bij het formuleren van het actie programma was het, bij mij al bekend dat het natuur doel niet gerealiseerd zal worden. Aan het begin van het teeltseizoen worden tevens zwembadjes met een voor ieder winveld, heel grote inhoud gevuld. Dat zorgt voor extra grote mestverliezen naar de bodem en grote opbrengst depressies.
Al in 1973 heeft G.W. Bloemen dit geheel nader uitgewerkt, voor het winveld 't Klooster, door een aparte transportverlaging te schetsen voor het rustseizoen (I) en het teeltseizoen (II).
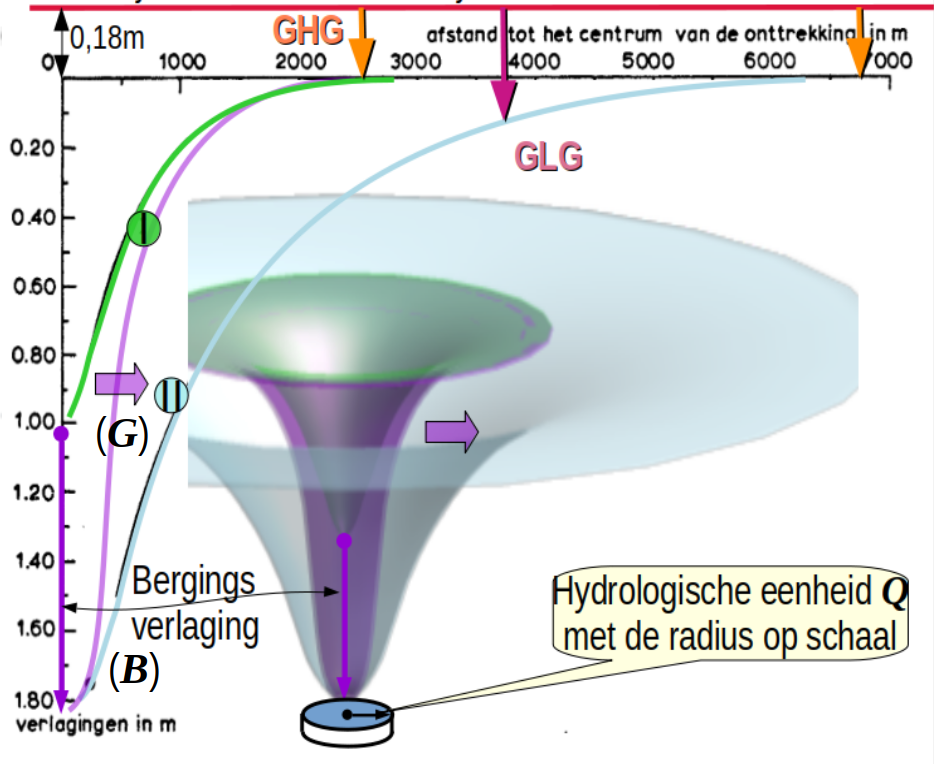
Ik heb dit nader uitgewerkt door 3D afbeeldingen te maken van de transportverlaging en de winningsverlaging in de vorm van een constante waarde van 0.2m, toe te voegen. Daardoor neemt de verlaging van het winveld, bij de pompput, toe tot een waarde van 2.0m.
Versterking A/a
Het winveld heeft een intrinsieke versterking A/a die bij de hier gehanteerde schaal kortstondig de waarde 21
aanneemt, waardoor de grondwaterspiegel
h(x,y,t) in dit voorbeeld, heel snel een overgang maakt, van 1.2m naar 2m.
Golfvoortplanting
Daarna ontstaat er als gevolg van herverdeling van grondwater een golf voortplanting, die we ook kennen van het eerste halve jaar van de vijf jaar dat de transporttrechter gewonnen werd. Dat detail is niet goed verwerkt door G.W. Bloemen, die z'n tijd overigens ver vooruit was.
Het debiet Q kan best veranderen op een grotere tijd (t) schaal (T), maar dat gaat wel minder snel. Daardoor weten we dat er in de jaarcyclus ook een verkleining van het debiet op zal treden met een ongeveer gelijke stap, daardoor keert de golfvoortplanting ook weer om.
Eliminatie transportverlaging
Bij de eliminatie van de transportverlaging gaat de versterkingsfactor groot A/a naar 1 gaat, bij de overgang naar een schadevrij winveld. Daarbij is er nog een mogelijkheid om het winveld te verbeteren. Bij de niet stationaire respons van het schadevrije winveld beweegt de grondwaterspiegel zich op en neer om een onbalans in
Q(t) ≈ Nwinbaar(t) A, op te kunnen vangen door het water in onbalans in de watervoerende laag over het volledige areaal A te bufferen.
De ontwerper heeft echter de mogelijkheid om een winveld met 21 cilinders
C(ρ) op te splitsen naar
n winvelden met
m cilinders, zoals 3x7 een 7x3 of een 21 x 1 configuratie. Daarbij worden de winvelden elk op een 2R radius afstand van elkaar geplaatst in plaats van de radius
R, om het beste dynamische gedrag te krijgen bij de laagste kosten, opdat het winveld beter het voortschrijdende gemiddelde van
h(x,y,t) kan volgen gedurende de jaarcyclus.
Horizontaal en lensvormig
Bij de bepaling van de schaal van de watervoerende laag zijn veel vrijheden om meerlaagssystemen te analyseren, waarbij scheidende (klei)lagen afgewisseld worden door watervoerende lagen. We beschouwen nu een natuurgebied zonder sloten waardoor het drinkwaterbedrijf de kwel als een extra bijdrage aan de winbare neerslag incalculeert, met daaromheen een landbouwgebied waarin sloten het grondwater afvoerden. In zo'n geval ontstaat in de nul-toestand een grondwaterlens, die de vorm heeft van een Gaussverhoging.
De winningsverlaging is in dit geval 0.4m, omdat eerst de grondwaterlens met 0.2m afgebouwd wordt. Daardoor is er geen kwel water meer dat als gevolg van de grondwaterlens naar de sloten in de omgeving uit zal treden, of bijdraagt aan de verhoging van de grondwaterspiegel. Daarna wordt een Gaussverlaging opgebouwd met een verlaging van 0.2m, waardoor de totale verlaging op 0.4m komt.