Prof. L.F. Ernst had aangegeven dat drinkwaterwinning voor gradiënten > 1‰, zeer sterk af te raden was. Bij het zoeken naar nieuwe winlocaties was er juist een sterke voorkeur voor plaatsen 'waar veel water te vinden was'.

In een hellend terrein, met een hellende grondwaterspiegel, zal een kwelstroom maar hoogst zelden uittreden, daarom spreek ik in dit geval liever over de onderstroom, die bij de drain alsnog overgaat in een zeer substantiële kwelstroom. Een maaiveld dat is ontstaan door verstuiving van zand, zal als regel heel goed de grondwaterspiegel volgen. Pionier gewassen ontwikkelen zich doordat zij mest kunnen opnemen door te wortelen in de onverzadigde zone, bovendien bevat een in de ijstijden gestuwde bodem vaak klei lagen die indertijd gevormd zijn en voor de gletsjer uit gestuwd werden. Daardoor worden dit soort landschappen door Nederlanders en ook vele Duitsers vaak als wonderschoon ervaren.

Ik verdeel nu de neerslag N, als volgt:

{α Nwinbaar, Nassimilatie, (2 - α) Nonderstroom}

met als doel om het effect van een variatie in Nwinbaar, de hoeveelheid te winnen water te kunnen bestuderen.
Voor α = 0 beschrijft dit de nul-toestand, α = 1 beschrijft de situatie bij winning, α < 1 is een voldoende voorwaarde die zeker stelt dat de onderstroom op peil blijft, α < 2 is een voldoende voorwaarde (de synthese kan verder, maar wel binnen beperkende voorwaarden), terwijl 2 < α is een noodzakelijke voorwaarde (door de overschrijding kan het natuur doel niet gerealiseerd worden).

We bestuderen in fig. 1. een gespreide winning in het winveld A met een onderstroom q(α)(x) die per cilinder ontstaat als qonderstroom = Nonderstroom a, maar ook berekent kan worden als een continue functie van x1 - x, waarbij de onderstroom als kwel uittreedt voor x=x0. Ik bestudeer alleen een zuiver parallelle stroming in het winveld A, waardoor ik kan volstaan met een doorsnede langs de x-as.

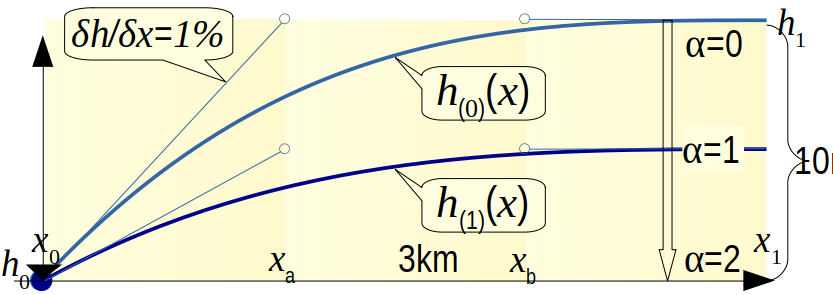
In fig. 1 en 2. zien we voor het eerst hoe de doorgaande trend ontstaat. Merk op dat er op x0 een scharnierende bovenrandvoorwaarde ontstaat door de overgang van de onderstroom naar overvloedige kwel. Het effect van de doorgaande trend moet niet onderschat worden, want winning van  1/3 van de neerslag, α=1, heeft als effect dat de stationaire hoogte van de grondwaterspiegel ten opzichte van h0, in het hele drain ... source interval halveert. Daarbij gaat de waarde bij de source van 10m naar 5m voor, een winveld (fig. 3), als de Slenk van Reutum. Het maakt bovendien ook weinig verschil of de 4 pompputten, van de lijn winning, met hun debiet Q (α)/4 (t) alle op x0 worden opgesteld, of gespreid over het winveld want op de ene of de andere manier wordt het debiet aan het winveld A, in het interval x0 ... x1, onttrokken. Omdat we niet precies (willen) weten, hoe dat zit, als er sprake kan zijn van een systeem met meerdere watervoerende lagen, is het van groot belang dat we kunnen beschikken over een winveld dat robuust schaalbaar is en zich adaptief aanpast aan de gegeven situatie.

Het ontstaan van de doorgaande trend is een gevolg van het gedeeltelijk leegtrekken van de bestaande grondwaterbel. Dit proces kan een beetje vergeleken worden met de vorming van een transporttrechter, zij het dat nu de gradiënten die het transport mogelijk maken juist kleiner worden, terwijl ze juist even groot moeten blijven. Door het water op de juiste plaats (x,y) terug te voeren kunnen we de artesische druk voor alle plaatsen (x,y) en alle tijdstippen (t) in het winveld, afgezien van een kleine winningsverlaging met daarop een kleine amplitude, als bij het geval horizontaal, op peil houden.

Maar waar halen we het infiltratie water dan vandaan? Ja die vraag had ik al verwacht, maar bij winning gestuurd door infiltratie is het debiet dat wordt geïnfiltreerd, gelijk aan het debiet dat wordt gewonnen, vooropgesteld dat de neerslag N constant is.

ontstaat er evenveel kwel bij de drain dan er wordt gewonnen. Het is dat kwel water, dat als een deel van de onderstroom onder het winveld rondgaat, en gespreid over het winveld teruggevoerd wordt. Dit is een enorm gunstige manier van werken, omdat het ook werkt in de hoge zandgebieden. Het is niet nodig om lange transportbuizen te maken om water uit de grote rivieren te infiltreren. Je kunt zo zelfvoorzienende winvelden maken, met een gedrag dat veel lijkt op het eerder besproken geval horizontaal. Cruciaal daarbij is dat we een circulaire grondwaterstroom zonder verliezen gebruiken om de hoogte van de grondwaterspiegel h(x,y,t), op peil te houden.

Bij dat proces wordt bij de drain, op x = x0, op een plaats met een bovenrandvoorwaarde aan de rand van A water gewonnen, op een zonder dat de hoogte van de grondwaterspiegel blijvend aangetast wordt, dat is mogelijk doordat er water dat als kwel zou uittreden, wordt gebruikt om te voorkomen dat de grondwaterbel in zal zakken.

Bij de Slenk van Reutum is de kwelstroom bij de drain zelfs 5 a 6x groter dan de onderstroom die bij elke andere cilinder C(ρ) passeert. Door de beschreven infiltratie treedt het grondwater bij de drain, zonder te pompen, door de artesische druk, moeiteloos uit.

We willen echter niet perse een gespreid winveld realiseren, of werken met een homogene watervoerende laag. Het gaat erom dat het natuur doel gerealiseerd zal worden. Daarbij mogen we de hoogte van de grondwaterspiegel slechts minimaal veranderen. Naar analogie met het geval horizontaal willen we nu voor het stationaire geval, de verlaging van de grondwaterspiegel uit de nul-toestand, waar mogelijk beperken tot een afstand van 0.2m. Ook voor het dynamische geval moet het winveld A + B in staat zijn om alle fluctuaties optimaal op te vangen met overal een minimale amplitude die afhangt van de actuele statistische eigenschappen van de neerslag N. Ondanks het feit dat de Laplace voorwaarden niet worden voldaan door dunne watervoerende lagen, kent de dunne watervoerende laag wel een voorspelbaar gedrag. De neerslag N(x,y,t) zorgt voor elke plaats (x,y) op een schaal X en op elk moment (t) op een schaal T, voor een aanwas van de grondwaterspiegel h(x,y,t). Omdat de onderstroom afgezien van de vorming van een kwelstroom bij de drain, verliesvrij is, hebben we door middel van de hoogte van de grondwaterspiegel h(X,T)(x,y,t) op de schalen (X,T) al veel kennis over het toekomstige gedrag van het systeem,