Eenduidigheid volgens Nyquist-Shannon
Tijdreeksen x [k] zijn uitsluitend nuttig als representatie van een signaal x (t), als x (t) eenduidig, via x (kT) met T een vaste periode lengte, uit de rij x [k] gereconstrueerd kan worden. Bij audio toepassingen, wordt het spectrum van het inkomende signaal begrensd door een voorfilter met een continuetijd puntspreidfunctie van de 2vorm sinc (t) = sin (t) / t.
Daardoor wordt het spectrum van het gegeven signaal
x
(t) in frequentie begrensd, waardoor we
met
iets meer dan 2 meetwaarden per periode T kunnen werken. Aan deze eenduidigheidsvoorwaarde wordt bij hydrologische toepassingen nooit veel aandacht besteedt, waardoor niemand nog weet wat goed is en waardoor er als gevolg van aliassen, fouten worden gemaakt. Dat maakt het opsporen van fouten op voorhand een onmogelijke opgave. Prof. F.C. van Geer noemt deze problemen overigens wel bij z’n
3inaugurele rede, maar TNO gebruikt geen hulpmidelen die het spectrum beperkt van de meetwaarden tot de basisband, gegeven door de sinc functie.
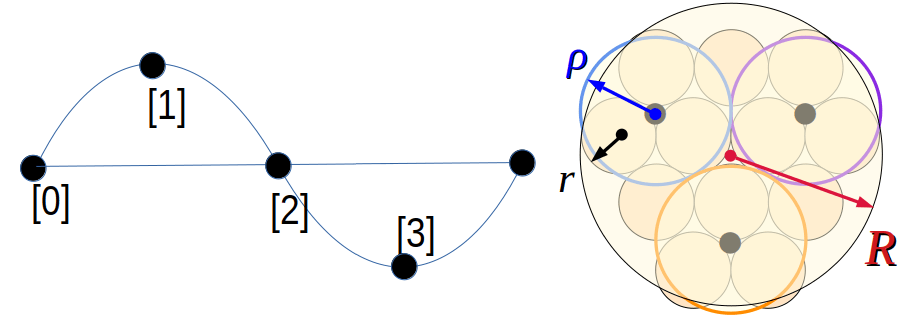
a) Het minimale aantal samples b) Plaatsing van peilfilters in het (x,y) vlak
Maar let goed op, het is voor zinvol onderzoek ook niet toegestaan om zo’n voorfilter toe te passen bij metingen aan dunne watervoerende lagen, omdat we bij de meting in dat geval te doen hebben met een effect dat ontstaat doordat de meetwaarden, vanwege het voorfilter voor een deel voldoen aan de Laplace voorwaarden terwijl de meetwaarden ook voor een ander deel juist niet voldoen aan de Laplace voorwaarden, vanwege de eigenschappen van de watervoerende laag. Door niet 2, maar 4 metingen te doen tijdens een periode, en geen andere algoritmes te gebruiken, kunnen we in (x,y) gebruik maken van de eigenschappen van de watervoerende laag en in (t) van de onverzadigde zone, om de benodigde eenduidigheid te realiseren.
Hiermee hebben we nu een techniek beschreven om een grondwaterspiegel foutloos te meten en ook foutloos te reconstrueren waarbij geen gebruik gemaakt wordt van de Laplace voorwaarden. Meetfouten behoren nu tot het verleden.
- Wikipedia: Bemonsteringstheorema van Nyquist-Shannon
- Wikipedia: Sinc-functie
- F.C. van Geer, Weet wat je meet en meet wat je niet weet, Oratie UU



