In de omgeving van de pompput(ten) verandert de richting waarin het grondwater stroomt zeer snel, in afhankelijkheid van lokale drukverschillen, die ontstaan als gevolg van de onbalans tussen N (t) en Q (t), waarbij het grondwater via een elementaire Gaussverlaging/verhoging in de centrale cilinder C_(ρ) via de paarse verlaging/verhoging, in een tijdsinterval van ±1 maand elk halfjaar van de ene ‘quasi-stationaire oplossing met golfvoortplanting’ naar de andere gaat. ¹Bloemen wist in 1973 ook wel dat er een golfvoortplanting optreedt in het winveld, en hij gaf aan dat het winveld radiaal symmetrisch moest zijn, met een oppervlak dat zowel continue is in de waarde en de 1^e en 2^e afgeleide, maar hiervoor zijn voor een willekeurig verloop van N (t) en Q (t) geen analytische oplossingen beschikbaar, afgezien van een beschrijving met de waterbalans die ir. G.W. Bloemen zelf introduceerde & de schaal transformatie die ik nog zal uitwerken.

Bij het voorbeeld dat hij uitwerkt, neemt hij aan dat alle neerslag N in het winterhalfjaar valt.

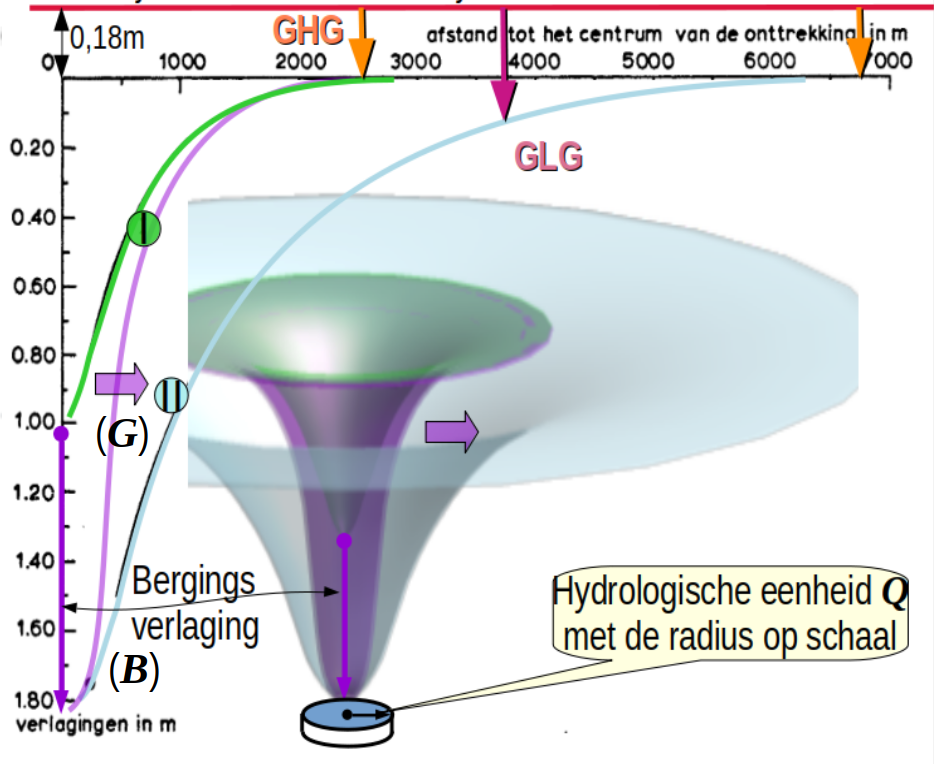
Opvallend bij z’n uitwerking is dat hij ook nog een extra verlaging, de winningsverlaging, vindt met een gemiddelde waarde van 0.18m waarvoor hij zo snel geen verklaring had. De tijd om dit beter te analyseren heeft hij ook niet gekregen, want prof. R.A. Feddes heeft hem laten werken aan kleinere compensatievergoedingen die mogelijk zijn bij het inbrengen van humus in de bodem. Ik heb die waarde van 0.18m boven de as uitgezet. Interessant is dat ir. J. Blom, als medewerker van het RID, als eerste een ¹afleiding heeft gegeven voor de winningsverlaging van een puntwinning in een watervoerende laag met een deklaag van klei. Gelijktijdig was het echter ook het RID dat het valse RID/RIVM monitoring programma introduceert, waarbij de diepte ontwatering wordt ‘vergeten’ als causale oorzaak voor het uitspoelen van o.a. mest.

Er kunnen natuurlijk niet twee grondwaterspiegels gelijktijdig bestaan. Om duidelijk te kunnen maken wat er gebeurt, is een animatie nodig. Het is al wel een beetje duidelijk hoe die eruit zal zien. De twee getekende grondwaterspiegels zullen voor het gegeven scenario, de extremen zijn waarbinnen de grondwaterspiegel zich beweegt, en de tijdconstante τ, bepaalt, gegeven de lengte van de jaarcyclus, hoever het golfverschijnsel zich voortplant, daarbij gedraagt een puntwinning zich ook anders dan een lijnwinning doordat de effectieve winningsstraal R(t) van een puntwinning het interval {ρ .. ρ_max} doorloopt en daarbij steeds groter en kleiner wordt bij het toe en afstromen van het ‘golffront’. Dichtbij de pompput en in het verre (win)veld, zal het grondwaterstandsverloop h_(x,y)(t) enige overeenkomst hebben met de blokgolf en de driehoeksgolf, die bij de bistabiele relaxatie oscillator zo’n belangrijke rol spelen, en aan het begin van het teeltseizoen zal, vanwege het schaal effect, bij een grote onbalans een zeer grote bergingsverlaging ontstaan (paars in de figuur) rond de centrale pompput. Met de beschrijving van de grondwaterspiegel h(x,y,t) die ik zojuist heb gegeven heb ik de animatie van het vlak V(x,y,h)(t) beschreven. Wie tegenwoordig computerspelletjes ziet, weet dat een animatie meer zegt dan duizend woorden. Maar in 1973 was de ontwikkeling van de (elektrotechniek en de fysica) nog niet zover gevorderd dat G.W. Bloemen daar toen al z’n voordeel mee kon doen. Daarom is het nodig om eerst de theorie van dunne watervoerende lagen, die niet voldoen aan de Laplace voorwaarden, verder uit te breiden om betere uitspraken te kunnen doen.

1. G.W. Bloemen, De berekening met een waterbalansmodel van de daling van freatisch grondwater als gevolg van grondwater winning, ICW Nota 758, aug. 1973
2. J. Blom, Verlagingen van het freatisch vlak bij grondwater-onttrekking in een gebied met vrije afwatering. RID Mededeling 74-7 (1973). Rijksinstituut voor Drinkwatervoorziening.`